分布数え上げソート [Counting Sort]
分布数え上げソートはソート対象のデータをキーにして、キーの出現回数とその累積度数分布を計算して利用することで整列を行うアルゴリズムです。 バケットソートと同じくキーとなるデータがとりうる値の範囲をあらかじめ知っている必要があります。バケットソートとの違いはキーの重複に対応したアルゴリズムであるということです。
アルゴリズム分析
前提としてソート対象のデータは 0 から 5 の整数とします。ソート対象の配列Aを {5,3,3,1,4} としておきます。
- キー(配列Aのデータ)を数え上げるための配列Cとソートのための作業用配列Bを用意する
- 配列Aのデータの出現頻度を数える(配列Cを利用)
- キーの累積度数分布を求める(配列Cが保持)
- (配列Cの)累積度数分布に従って配列Aから配列Bにデータをコピーする
- (必要なら配列Bから元の配列Aにデータをコピーする)
表を交えて解説します。
手順2〜3を表にしてみると以下のようになります。手順2では配列Cのキーが表の左の列になり、値が真ん中の列になります。手順3ではキーはそのままで値が右の列になります。
| データの範囲(キー) | キーの出現回数(X) | 出現回数の累計(Y) |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 1 | 1 |
| 2 | 0 | 0 |
| 3 | 2 | 3 |
| 4 | 1 | 4 |
| 5 | 1 | 5 |
分布数え上げソートはキーの重複に対応しているといいました。キーが重複しているのは 3 です。整列後のふたつの 3 の位置(配列のインデックス)は 「Y - X」 と 「Y - 1」 で計算できます。この例だと「3 - 2 = 1」と「3 - 1 = 2」になります。
実際のプログラミングでは重複したキーの位置の計算は、作業用配列Bにコピーする時に(手順4で)配列Aの後ろから前へコピーしていくことで簡単に実装できます。
図解
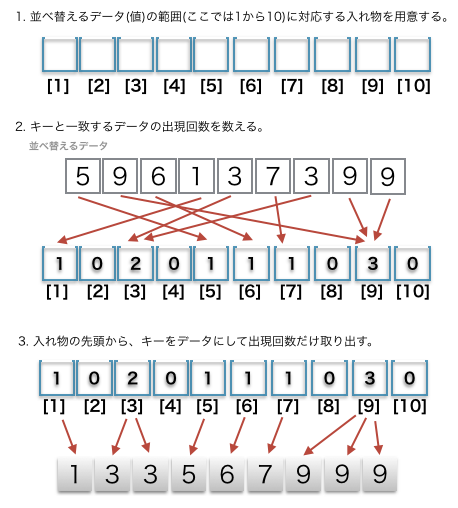
特徴
バケットソートと同じくソート対象のデータがとりうる値の範囲をあらかじめわかっていなければなりません。作業領域もキーの個数を数えるための領域と結果を格納する領域が必要になります。あまりに大きな範囲のデータを取り扱うには RAM などに限度があるので物理的に不可能になります。しかし大きな作業領域と引き換えにデータの大小を比較しなくてよいので高速な整列処理を実現できます。
サンプルコード
C言語
配列を昇順に整列させます。
/* キーは0からMまでの範囲の整数 */
#define M 10
/* 作業用配列 (N は配列の要素数) */
int work_data[N-1];
/* キーの分布を数え上げるための配列 */
int count[M+1];
/*
分布数え上げソート
配列aを整列する。結果は配列bが保持する。
@param int a ソート対象の配列
@param int b 作業用の配列
@param int n ソート対象の配列の要素数
*/
void counting_sort(int a[], int b[], int n)
{
int i;
/* カウンタ(キーの出現回数)を初期化 */
for (i = 0; i <= M; i++)
count[i] = 0;
/* キーの出現回数 */
for (i = 0; i < n; i++)
count[a[i]]++;
/* 数え上げたキーの累積度数分布 */
for (i = 0; i < M; i++) {
count[i+1] += count[i];
}
/* 度数分布に従ってデータを配列aから配列bにコピーする */
for (i = n - 1; i >= 0; i--) {
b[--count[a[i]]] = a[i];
}
}
分布数え上げソートのデモンストレーション プログラム: counting_sort.c
Python
上記のC言語の実装とは異なり、累積度数分布は作成せずに最後の for 文で値の出現回数だけ繰り返すことでリストを並べ替えます。
# -*- coding: utf-8 -*-
def counting_sort(array, maxval):
m = maxval + 1
count = [0] * m # 度数分布のリストをゼロで初期化
for a in array:
count[a] += 1 # 出現回数の計算
i = 0
for a in range(m): # 値の最大値まで繰り返す
for c in range(count[a]): # 値の出現回数だけ繰り返して元のリストに値をコピーする
array[i] = a
i += 1
return array
if __name__ == '__main__':
from random import shuffle
maxval = 15
l = [1, 1, 2, 3, 4, 4, 5, 6, 7, 8, 8, 8, 10, 10, 12, 14, 14, 15]
lcopy = l[:]
shuffle(l)
print('Unsorted')
print l
assert l != lcopy
print ('Sorted')
print counting_sort(l, maxval)
assert l == lcopy
