本ページには広告・プロモーションが含まれています。

度数分布

度数分布の説明

度数分布とは何かが発生する頻度(度数)をまとめたものである。 一般的に 度数分布表 という表を作成する。

何かというのは専門用語では 階級 と言う。 グループとか項目と同じ意味。

階級が数字の場合は 階級幅 を設定してデータの区間を設定することができる。 階級の区間において階級を代表する値は 階級値 と呼ぶ。

ナンバーズでは抽せん数字を0から999の数字ととらえることで 階級を「0〜99」「100〜199」のように階級を100ごとに区切って出現回数を調査できる。 このときの階級幅は100となり、階級の真ん中の値が階級値となる。

階級値 = (階級の初め値 + 階級の終わりの値) / 2

度数分布表というのは統計学においてデータを整理するための 基本中の基本 でとても大切。

また度数分布表をもとに作成されたグラフを ヒストグラム と呼び、視覚的にデータの分布を把握できる。

度数分布表の例

「抽せん数字」を階級にした度数分布表

ナンバーズ3の第1回から第4170回の抽せん数字を用いて、度数(当せん回数)が多い抽せん数字を10個。

度数(当せん回数)
抽せん数字(階級)
618 11
638 11
845 10
908 10
703 10
943 10
198 10
199 10
589 10
928 10

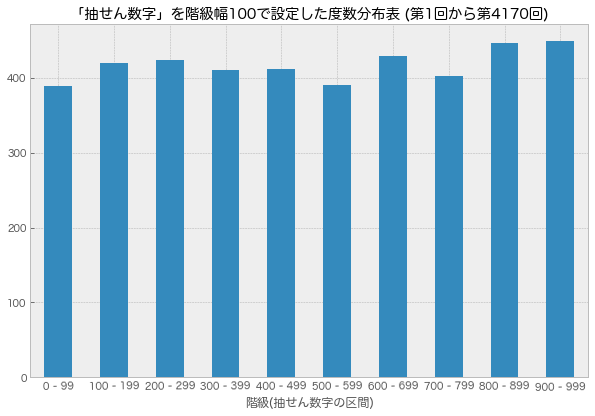
「抽せん数字」を階級幅100で設定した度数分布表

第1回から第4170回の抽せん数字で集計。

階級(抽せん数字の区間) 階級値 度数(当せん回数)
0 - 99 49.5 389
100 - 199 149.5 420
200 - 299 249.5 423
300 - 399 349.5 410
400 - 499 449.5 412
500 - 599 549.5 390
600 - 699 649.5 429
700 - 799 749.5 402
800 - 899 849.5 446
900 - 999 949.5 449

度数の棒グラフを作成することで視覚的に度数の違いを把握する。

度数分布表の棒グラフ

相対度数、累積度数、累積相対度数

  • 相対度数は1つの階級の度数が、すべてデータの度数の合計のうちどれくらいの割合を示すもの
  • 累積度数は階級ごとの度数を足しあわせた値
  • 累積相対度数は階級ごとの相対度数を足し合わせた値

上で示した『「抽せん数字」を階級幅100で設定した度数分布表』に相対度数、累積度数、累積相対度数を追加してみます。

「抽せん数字」を階級幅100で設定した度数分布表 (第1回から第4170回)
度数(当せん回数) 相対度数 累積度数 累積相対度数
階級(抽せん数字の区間)
0 - 99 389 0.093285 389 0.093285
100 - 199 420 0.100719 809 0.194005
200 - 299 423 0.101439 1232 0.295444
300 - 399 410 0.098321 1642 0.393765
400 - 499 412 0.098801 2054 0.492566
500 - 599 390 0.093525 2444 0.586091
600 - 699 429 0.102878 2873 0.688969
700 - 799 402 0.096403 3275 0.785372
800 - 899 446 0.106954 3721 0.892326
900 - 999 449 0.107674 4170 1.000000

累積度数は上から順に度数を合計したものとなっている。そのため、最後の階級(ここでは「900 - 999」)の累積度数は度数の合計となり、累積相対度数は 1.0 となる。

それぞれの計算式:

相対度数 = 階級の度数 ÷ 度数の合計

累積度数 = 階級(n番目)の度数 + 階級(n-1番目)の度数

累積相対度数 = 階級(n番目)の相対度数 + 階級(n-1番目)の相対度数

ナンバーズの予想に使うには

ナンバーズの予想に度数分布表をどのように使うのか？

それは抽せん数字の出現傾向を把握するためだ。

単純に抽せん数字ごとに出現回数を集計した場合、 上の表を参考にすれば「過去に638が当選しやすい数字だから、次回も638を買おう」と予想できる。

ただこれではデータの傾向が大雑把なので、 抽せん数字に与えるであろう要因を絞り込んだ度数分布表 が求められるはず。

例えば

  • 曜日ごとの抽せん数字の出現傾向
  • 月ごとの抽せん数字の出現傾向
  • 位ごとの抽せん数字の出現傾向

といった具合に度数分布表を作るという作業は、どのような視点でデータを把握したいのかを考える必要がある。

度数分布表の内容によって予想番号にも違いが出てくる。


最終更新日: 2020年01月05日(日)


目次

プロローグ

統計解析

データマイニング

資料集

Back to top