本ページには広告・プロモーションが含まれています。

移動平均

移動平均の説明

移動平均とは 時系列データ の値の変化を滑らかにする方法です。

一定の区間を定めてその区間内の平均値を計算したものが移動平均の値になります。 平均することで値の変動を打ち消す効果があるので、時系列データの傾向が読み取りやすくなります。

例えば毎月のデータについて12ヶ月ごとの変動をわかりやすくしたい場合には区間を12ヶ月(データ数が12個)とした移動平均を計算すると、 1年間(12ヶ月単位)の周期が明らかになるなどの分析結果を得ることができます。

移動平均には種類があります。

単純移動平均
一定区間のデータを平均したもので、一般的に移動平均といえば単純移動平均のことを指す。
加重移動平均
時点ごとに異なるウエイト(重み)を反映して平均を算出したもの。
指数移動平均
指数関数的にウエイト(重み)を減少させて平均を算出したもの。

さらに平均するデータの区間の取り方も方法が分かれます。

後方移動平均
ある時点とそれ以後のデータの平均値を使う方法。
前方移動平均
ある時点とそれ以前のデータの平均値を使う方法。
中央移動平均
ある時点とその前後のデータの平均値を使う方法。

単に「移動平均」といった場合は単純移動平均の後方移動平均を指すことが多いようです。


単純移動平均の計算方法

ここでは単純移動平均について説明します。

まずは実際の移動平均値を下記の表に示します。 4141回から4150回のミニの抽せん数字を5回分の移動平均(後方・中央・前方)と4回の中央移動平均を計算したものです。

※抽せん数字は本来質的データですが量的データとして扱っています。

抽せん数字 ミニ 5回 後方移動平均 5回 中央移動平均 5回 前方移動平均 4回 中央移動平均
回号
4141 56 NaN NaN 49.4 NaN
4142 0 NaN NaN 56.4 NaN
4143 95 NaN 49.4 63.0 53.00
4144 61 NaN 56.4 59.2 47.75
4145 35 49.4 63.0 53.8 70.50
4146 91 56.4 59.2 62.2 55.00
4147 33 63.0 53.8 NaN 58.75
4148 76 59.2 62.2 NaN 58.50
4149 34 53.8 NaN NaN 55.00
4150 77 62.2 NaN NaN NaN

上の表は 前準備 で用意した python のデータフレームを使って作成しました。

# ミニのデータを作る
df['mini'] = df['place10'].astype(str) + df['place1'].astype(str)
df['mini'] = df['mini'].astype(int)

# 移動平均のデータフレーム
data = {'抽せん数字 ミニ': df.loc[4141:4150, 'mini'],
      '5回 後方移動平均': df.loc[4141:4150, 'mini'].rolling(window=5).mean(),
      '5回 中央移動平均': df.loc[4141:4150, 'mini'].rolling(window=5, center=True).mean(),
      '5回 前方移動平均': df.loc[4141:4150, 'mini'].rolling(window=5).mean().shift(-4),
      '4回 中央移動平均': df.loc[4141:4150, 'mini'].rolling(window=4, center=True).mean()}
ma_df = pd.DataFrame(data)
ma_df.index.name = '回号'

後方移動平均

後方移動平均は基準となる時点より後方の区間を用いた平均値です。

抽せん数字 ミニ 5回 後方移動平均
回号
4141 56 NaN
4142 0 NaN
4143 95 NaN
4144 61 NaN
4145 35 49.4
4146 91 56.4
4147 33 63.0
4148 76 59.2
4149 34 53.8
4150 77 62.2

4141回から4144回は過去(後方)のデータが５回より不足しているので NaN となっています。

4145回には自身を含めて過去５回(4141回から4145回)の平均値が入ります。

49.4 = (56+0+95+61+35)/5

4146回には4142回から4146回の平均値が入ります。

56.4 = (0+95+61+35+91)/5

中央移動平均

中央移動平均は基準となる時点の前後を用いた平均値です。

抽せん数字 ミニ 5回 中央移動平均
回号
4141 56 NaN
4142 0 NaN
4143 95 49.4
4144 61 56.4
4145 35 63.0
4146 91 59.2
4147 33 53.8
4148 76 62.2
4149 34 NaN
4150 77 NaN

4141回と4152回、そして4149回と4150回は前後のデータが５回より不足しているので NaN となっています。

4143回は自分を中心にした前後2回ずつの(4141回から4145回)の平均値が入ります。

49.4 = (56+0+95+61+35)/5

4144回には4142回から4146回の平均値が入ります。

56.4 = (0+95+61+35+91)/5
中央移動平均で区間が偶数個の場合(4回 中央移動平均)
抽せん数字 ミニ 4回 中央移動平均
回号
4141 56 NaN
4142 0 NaN
4143 95 53.00
4144 61 47.75
4145 35 70.50
4146 91 55.00
4147 33 58.75
4148 76 58.50
4149 34 55.00
4150 77 NaN

区間が偶数個の場合、中央の区間に該当するデータ(4142回と4143回のあいだの4142.5回という回号)がありません。

表には4回分の中央移動平均を計算していますが pandas の rolling メソッド で計算したもので、中央の回号は 「項目数 / 2 + 1」番目になります。

4143回の平均値として4141回から4144回の４回分の平均値が入ります。

53.0 = (56+0+95+61)/4

4144回の４回中央移動平均なら4142回から4145回の平均値が入ります。

47.75 = (0+95+61+35)/4

区間が偶数個の場合は 区間を前後にずらした平均値の平均 を用いる方法もあり、こちらの計算式が一般的なようです。

前方移動平均

前方移動平均は基準となる時点より前方の区間を用いた平均値です。

抽せん数字 ミニ 5回 前方移動平均
回号
4141 56 49.4
4142 0 56.4
4143 95 63.0
4144 61 59.2
4145 35 53.8
4146 91 62.2
4147 33 NaN
4148 76 NaN
4149 34 NaN
4150 77 NaN

4147回から4150回は前方のデータが５回より不足しているので NaN となっています。

4141回には前方５回(4141回から4145回)の平均値が入ります。

49.4 = (56+0+95+61+35)/5

4142回には4142回から4146回の平均値が入ります。

56.4 = (0+95+61+35+91)/5

ナンバーズの予想に使うには

移動平均は時系列分析の手法ですから、抽せん数字を量的データとして扱うことで時間の経過と共に抽せん数字にどのような傾向や周期があるのかを分析することができます。

例えば、ナンバーズだと土日は抽せんが行われないので5日(5回)分の移動平均を分析することで、おおむね週次の傾向分析になります。

ミニの抽せん数字についての移動平均分析

第4001回から第4100回(全部で100回分)のミニの抽せん数字を移動平均をグラフで描いて傾向を分析してみます。

python のプログラムは 前準備 で用意したデータフレームを使っています。

まずはミニの抽せん数字を時系列データとしてグラフに描いてみます。 横軸 x が回号、縦軸 y が抽せん数字になります。

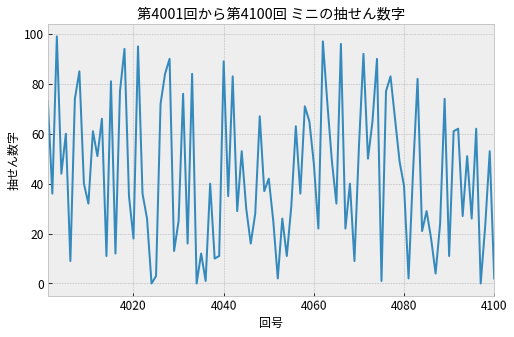
第4001回から第4100回のミニの抽せん数字


上のグラフから読み取れること:

  • 抽せん数字は乱高下を繰り返している
  • 4050回あたりは抽せん数字が40以下の小さな数字がよく出現していそう

次に10回の後方移動平均をグラフに描いてみます。

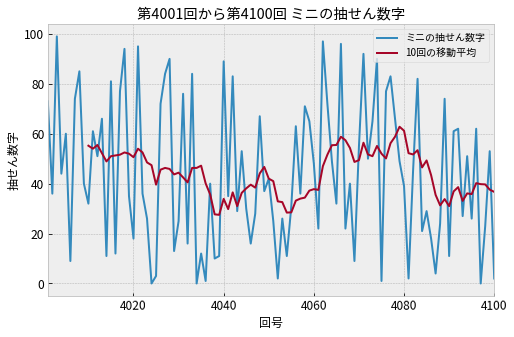
第4001回から第4100回のミニの抽せん数字 (10回後方移動平均付き)


上のグラフから読み取れること

  • 4020回から4040回くらいまでは抽せん数字が小さくなる傾向がある
  • 4060回以降4080回ぐらいまでは数字が大きくなる傾向がある
  • 10回分の抽せん数字の平均値は60よりも低い傾向がある
  • 規則的な変動はなさそう

さらに50回の後方移動平均をグラフに描いてみます。

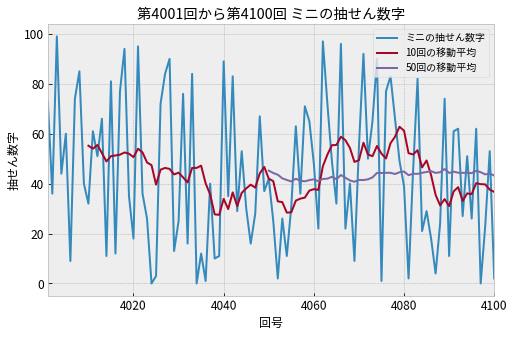
第4001回から第4100回のミニの抽せん数字 10回移動平均と50回移動平均


上のグラフから読み取れること

  • 50回という中長期間では抽せん数字に大きな変動はない
  • 抽せん数字の平均値は40から50の範囲にある
  • 周期的な変動はなさそう

以上、移動平均を用いた時系列分析の例でした。

移動平均の区間を 1 や 2 のように小さな区間を取れば自分自身と同じ傾向が現れるため分析に使えないデータとなってしまうので注意しましょう。

自分自身の過去のデータから周期や傾向を分析したい場合には 自己相関分析 を使います。


最終更新日: 2020年01月16日(木)


目次

プロローグ

統計解析

データマイニング

資料集

Back to top