本ページには広告・プロモーションが含まれています。
時系列解析
時系列解析の説明
時系列解析とは 時間の経過と共に記録されたデータについて傾向、周期、誤差を分析する 手法を指す。
時間の経過と共に記録されたデータのことを 時系列データ と言う。
時系列データから何かを読み取ろうとするとき、数字を眺めているだけではどうにもなりません。
時系列データから 基本的な統計量 を算出して、 「当せん金額が最も多かったのは先月だ」とか「抽せん数字の平均値は 555.5 だ」とかは理解できるが、 時間の流れに沿った特徴を読み取る のはデータを見ているだけではわからないのです。
そんな時系列データはグラフを描いて分析するのが常套手段です。
グラフから 傾向、周期、誤差 を読み取ります。
- 傾向:
- 増加や減少があるのか?増減は激しいのか、ゆるやかなのか?といった変動を見る。
- 周期:
- 増減の変動に一定の規則が現れているのかを見る。
- 誤差:
- 不規則な変動があるのかを見る。
ナンバーズの予想に使うには
まずは抽せん数字について色々な時系列データを作成してグラフを描いて、どのような変動が見られるのかを眺めてみるのが第一歩です。
例としてミニの抽せん数字について時系列データを解析してみます。
python のプログラムは 前準備 で用意したデータフレームを使っています。
# ミニのデータを作る
df['mini'] = df['place10'].astype(str) + df['place1'].astype(str)
df['mini'] = df['mini'].astype(int)
ミニの抽せん数字についての時系列分析
第4001回から第4100回(全部で100回分)のミニの抽せん数字をグラフで描いたのが下の図です。
# ミニのデータを作る
mini_graph = df.loc[4001:4100, 'mini'].plot(title='第4001回から第4100回 ミニの抽せん数字', figsize=(8, 5), rot=1, fontsize=8)
mini_graph.tick_params(labelsize='large')
mini_graph.set(ylabel='抽せん数字', xlabel='回号')
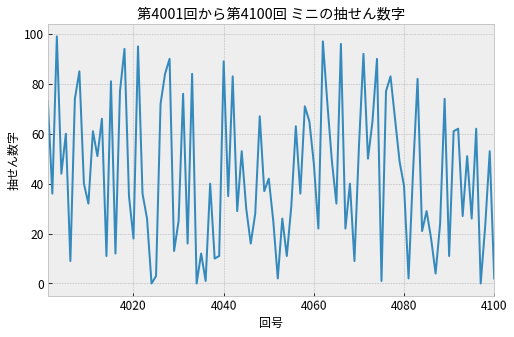
このグラフから読み取れること:
- 抽せん数字は乱高下を繰り返している
- 4050回あたりは抽せん数字が40以下の小さな数字がよく出現していそう
どうやらこのデータだけでは傾向や周期は読み取りにくいです。
そこで 移動平均 を計算して、同じグラフにプロットしたものが下の図です。
移動平均というのは時系列データをなめらかにする手法で、一定の区間を定めてその区間内の平均値を計算したものです。 詳しくは 移動平均 のページを参照。
今回は「10回毎の平均値」を計算して、赤いラインで描いています。10回分の平均値なので始めの4001回から4009回までのデータはありません。
# グラフ用にミニの抽せん数字と移動平均値だけのデータフレームを作る
ma_df = pd.DataFrame({'ミニの抽せん数字': df.loc[4001:4100, 'mini'], '10回の移動平均': df.loc[4001:4100, 'mini'].rolling(10).mean()})
# グラフ描画
ma_graph = ma_df.plot(title='第4001回から第4100回 ミニの抽せん数字', figsize=(8, 5), rot=1, fontsize=8)
ma_graph.tick_params(labelsize='large')
ma_graph.set(ylabel='抽せん数字', xlabel='回号')
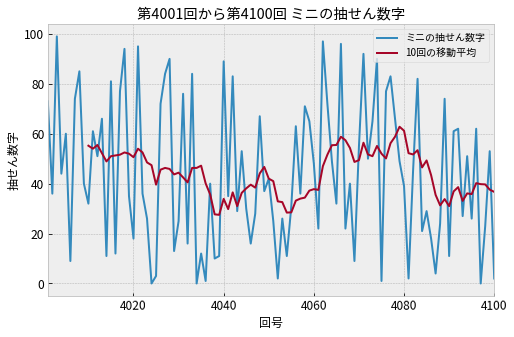
抽せん数字だけのグラフではわかりにくかった傾向が移動平均によって明らかになっています。
- 4020回から4040回くらいまでは抽せん数字が小さくなる傾向がある
- 4060回以降4080回ぐらいまでは数字が大きくなる傾向がある
- 10回分の抽せん数字の平均値は60よりも低い傾向がある
- 規則的な変動はなさそう
こうした分析結果にもとづいて抽せん数字の予想につなげます。
最終更新日: 2020年01月15日(水)
目次
プロローグ
- はじめに
- ナンバーズの予想・攻略方法
- 前準備 (ナンバーズ3のデータの準備と統計解析の環境について)
統計解析
データマイニング
- マルコフ連鎖 (ひとつ前の過去が未来を決定する)
- アソシエーション分析 (よくある組み合わせを発見する)
- 決定木 (要因を分析して未来を予測する)
- サポートベクターマシン (パターン認識)